أثناء الملاحة قد يتطلب الأمر حل رصدة للشمس أثناء النهار أوحل رصدة منفردة لنجم أثناء الشفق المسائى أو الشفق الصباحى للحصول على عناصر خط الموقع الفلكى وهما الإتجاه الحقيقى (True Bg.) و الفرق (Intercept). وكما هو معروف فإن الرصدة الفلكية تتكون من الوقت (UT) و الإرتفاع السدسي (Sext. Alt.)
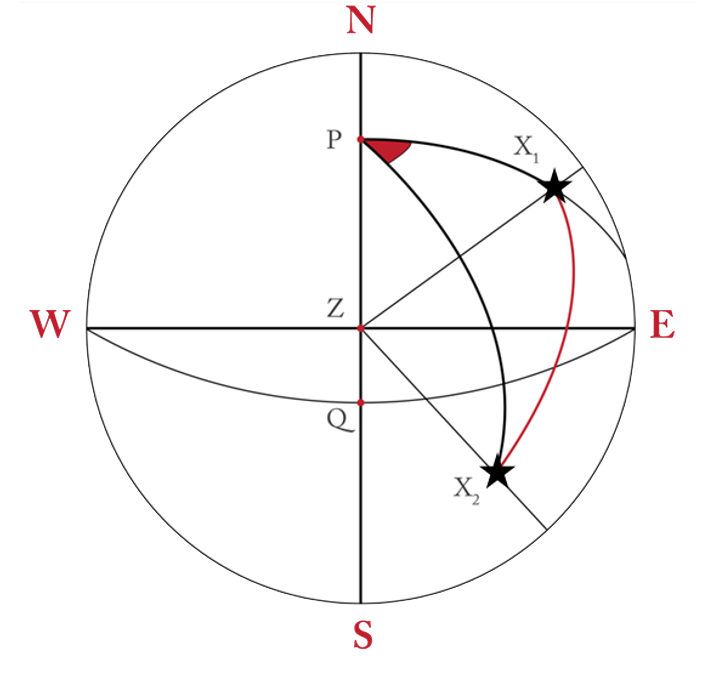
الشكل التالى يوضح تسلسل الحل للحصول على عناصر خط الموقع الفلكى والتى تم على أساسها تصميم البرنامج.
قم بتطبيقه الآن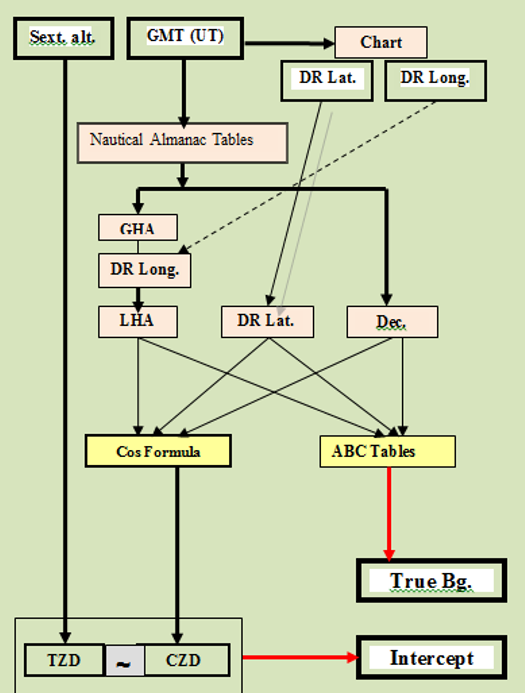
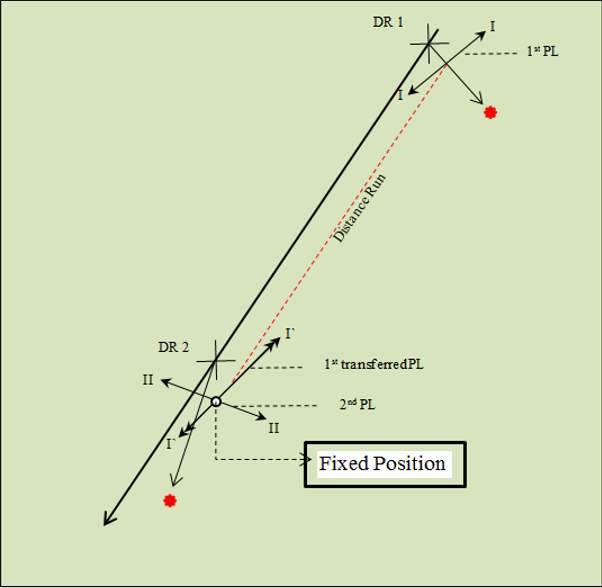
أثناء النهار لا يكون متاحا للرصد أى جرم سماوي عدا الشمس بالطبع لذلك فإن تحديد الموقع المرصود يتطلب رصدتين للشمس بينهما فترة إبحار طويلة نسبيا (تتحدد بتغير الإتجاه الحقيقى للشمس بحوالى 30 على الأقل) ومن ثم يتم إزاحة خط الموقع الأول حتى وقت خط الموقع الثانى حيث تكون نقطة تقاطعهما هى الموقع المرصود فى وقت الرصد الثانى الشكل يوضح هذا التصور لحل هذه المسألة..
وقد تم تصميم البرنامج كما يلى:
فى السنوات الأخيرة أصبح الكثير من أنظمة الملاحة الإكترونية خارج نطاق الخدمة خاصة تلك الأنظمة التى تعتمد على المحطات الأرضية وأصبح تحديد الموقع للسفن المبحرة يعتمد على منظومة GPS وبالتالى أصبح تحديد الموقع بإستخدام الملاحة الفلكية قليل الأهمية بل ويكاد يندثروذلك لعدة أسباب تتلخص فيما يلى : .
ولكن فى المقابل يمكننا إعتبار أن الملاحة الفلكية تتميز بما يلى :
أول من تعرض لفكرة الحل تحليليا بإستخدام حساب المثلثات الكروية هو اليوغوسلافى KOTLARIC وذلك فى عام 1954 حيث قام بنشر جداول لحل أزواج مختارة من النجوم الملاحية فى عام 1971. ولم يكتب لهذا الأسلوب النجاح لعدة أسباب هى:
فى الطريقة الحالية للحل التحليلى بإستخدام حساب المثلثات الكروية والتى أسميناها الطريقة المصرية يقوم الراصد بإدخال بيانات النجوم الملاحية التى تم رصدها (الوقت / الإرتفاع السدسى) بحد أقصى 7 نجوم وكذلك إحداثيات هذه النجوم المستخرجة من التقويم البحرى بالإضافة إلى البيانات التقليدية مثل خط سير السفينة وسرعتها والموقع الحسابى وفى نهاية برنامج الحل يحصل على الموقع المرصود الأكثر إحتمالا .
وقد تم تطبيق هذا الأسلوب عمليا أثناء الإبحار (1997)على سفينة التدريب عايدة 4 (التابعة للأكاديمية العربية للعلوم و التكنولوجيا والنقل البحرى) ومقارنته بالموقع الذى تم الحصول عليه من منظومة GPS وكانت النتائج فى الحدود المسموح بها .
البيانات التى يتم إدخالها :
تفصيل ذلك كما يلى.
الحسابات الرئيسية
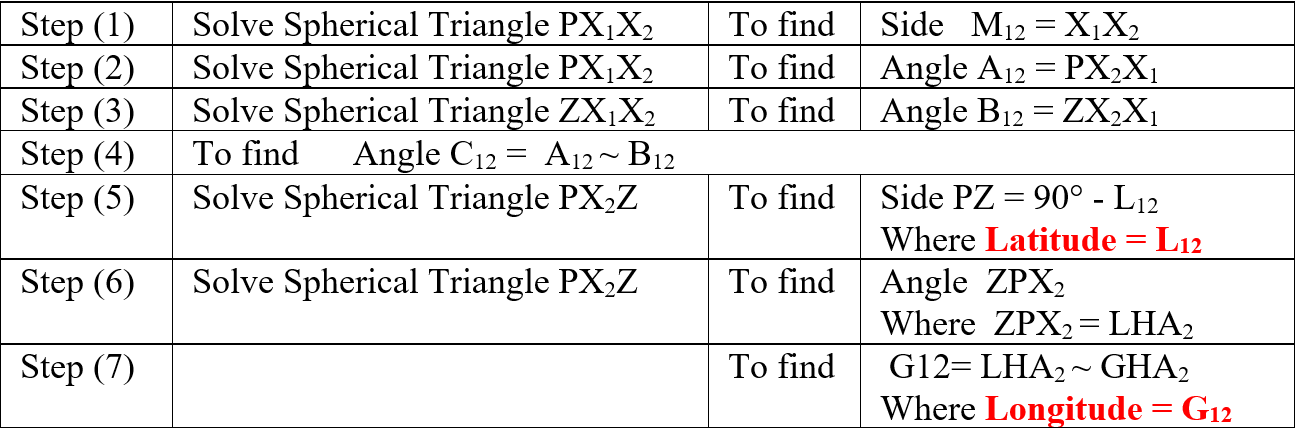
الجدول التالى يبين أزواج النجوم التى يتم حلها ؛ حيث أقصى عدد هو 21 حل فى حالة رصد 7 نجوم .
ولكن تم تصميم البرنامج بحيث يحذف حل زوج النجوم الذى يكون فرق إتجاهيهما 30° >أو محصورا بين (30° ± 180° ) ؛ بذلك قد يكون عدد الحلول > 21.
نفترض أن عدد أزواج النجوم ( Xi X j ) التى تم حلها هو n ؛ ولإيجاد الموقع المرصود الأكثر إحتمالا نكمل الحل كما يلى:
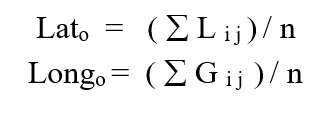قم بتطبيقه الآن
حتى بداية عصر الملاحة بإستخدام الأقمار الصناعية كانت الطريقة الأكثرشيوعا لإيجاد موقع السفينة المرصود الأكثر إحتمالا هى طريقة النقيب البحرى الفرنسي (لواء بحرى فيما بعد) مارك سانت هيلير التى نشرت فى سنة 1875 والتى عرفت بطريقة الفرق للسهولة.
تتلخص هذه الطريقة فى إيجاد مايسمى بعناصر خط الموقع الفلكى وهما الفرق و الإتجاه الحقيقى للجرم السماوى الذى تم رصده ومن ثم يمكن رسم خط الموقع الفلكى أى المحل الهندسى لموقع السفينة فى وقت تنفيذ الرصدة.
وتكمن عبقرية هذه الطريقة فى أنه مهما كان الخطأ فى الموقع الحسابى المستخدم فى الحل فإننا نحصل فى النهاية على نفس خط الموقع بشرط وحيد وهو التوقيع من هذا الموقع الحسابى.
من البديهى أنه لإيجاد موقع يلزم خطي موقع على الأقل ليتقاطعا فى نقطة تكون هى الموقع المرصود ولزيادة الدقة يلزم العديد من خطوط الموقع مع ملاحظة أن كل منها قد تم رصده فى وقت مختلف لذلك يجب أولا توحيد أزمنة الرصد لزمن واحد متفق عليه
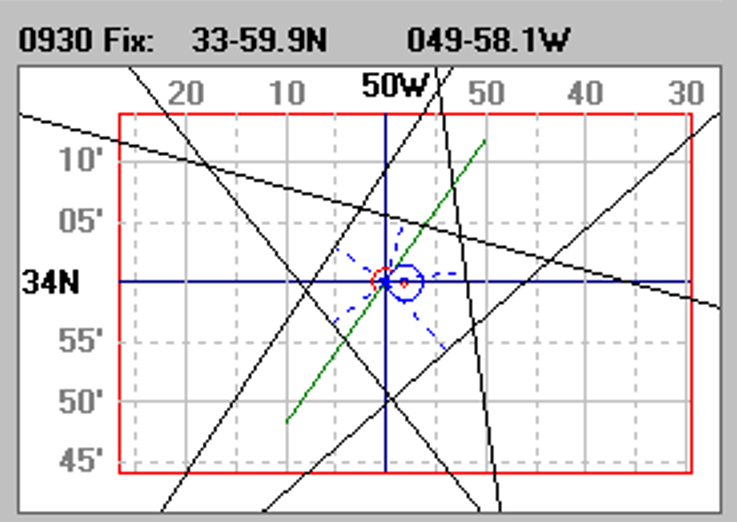
تأتى بعد ذلك المشكلة الأكبر وهى كيفية التعامل مع شبكة خطوط الوقع الناشئة من رسم الخطوط على الخريطة أو لوحة التوقيع )الشكل المرفق للتوضيح(.
البرنامج الحالى وهو ماأسميته الطريقة العامة (Universal Method) يحل هذه المشكلات المتتابعة وخصوصا كيفية التعامل مع شبكة خطوط الموقع المفترضة ومن ثم الحصول على الموقع المرصود الأكثر إحتمالا في الوقت المطلوب إيجاد الموقع فيه.
وقد تم مقارنة النتائج مع الموقع المفترض بنظام (GPS) فى الوقت المطلوب إيجاد الموقع فيه وكان الأختلاف لايتعدى (0.7 M) وهو بالنسبة للملاحين إختلاف طفيف جدا اُثناء الملاحة فى أعالى البحار.
